最近私の中で、博士後期課程(以下、単に博士課程と呼ぶ)への進学が以前ほど自明でなくなってきたように感じられるので、その思考を言語化することで、理由を捉え、将来を展望してみようと思います。
まず前提として私は、修士課程へ進学する際に、主に大学院入試の成績による事情で、4回生時の研究室とは異なる研究室(第二希望の研究室)に進学しました。その時点では博士課程への進学について、それほど意識していた訳ではありませんでした。ただ、M1に上がる瞬間の4月2日に阿蘇山へ登り、山中で何となく博士課程に行っても良いかもな、という啓示を受けました。配属後、研究室にはD1〜D3まで各学年1人ずつ博士課程の学生がおり、全員普通に元気そうだったので、この研究室で博士課程に進学しても、死ぬことは無さそうだなという印象を受けました。世の中には、ブラック過ぎて人が死ぬ大学や研究室があるという話も、何となく聞いたりしていましたので。
何というか博士課程に行く、そして博士号を取るという行為は、手段やプロセスに据えるべきであって、それ自体を目的化すると続かないのでは、という気がします。人間は楽しいこと、本当に興味のあることに没頭するものです。私が最近個人的にやっていて楽しいことは、相変わらずBTCUSDのチャートを眺めること、投資家の書いた本やブログを読むこと、ネオ・プラグマティズムについて書かれた哲学者の本を読むこと、などです。私は、高1の秋冬に理系を選択してからここまで、理系の進路をずっと進んできました。ただ、文理選択は自明に理系だったわけではありません。私は、高校生1年生の時、定期テストで物理や数学で40点以下の赤点を何度も取っていた一方、現代社会だけは学年トップ級の成績を連発していました。そのため、同じ学年の人間からは完全に文系に進むものと思われていました。また、理系に進んでみると、驚きの声が何度も聞かれました。実際、私は文理選択に際して、当時的には結構悩んだ末に進路を決定したのです。理系に進んでおけば後から文転するのは比較的容易である、というのは理由の1つですが消極的理由です。最終的に私の判断に大きく影響したのは、小中学生の時に6年間通っていた塾の恩師にアドバイスを求めに行った時だったと思います。小中学生の時の私は、どの科目も比較的バランス良くできる方でしたが、それでも国語や英語よりは、数学や理科の方が明らかに良く出来るタイプでした。また、小学生高学年の時分は、教室でずっと宇宙の話をしているような宇宙オタクでした。そのため、その頃の私のことをよく知る恩師からは、君は理系だと思う、というようなことを言われ、私もそうかと思って、理系に進むことにしました。
その後は、高校の時に通っていた塾での英語の指導が良く、高校を卒業する頃には、私の一番の得意科目は英語になっていました。物理や数学が苦手なのは、高校在学中にはほとんど改善しませんでした。
思えば私は、それ以降今に至るまで、特に何も考えることなく進路選択してきたのかもしれません。それは、ある意味幸福でさえあります。私は、高校を卒業する瞬間に、京大工学部を受験して落ちていますが、いま思うと、どういう深い理由があったのかは思い出せません。それは、深い理由が無かったからなのでしょう。何となく京大を受け、理系なので何となく工学部、くらいの気持ちで京大工学部を受けていたと思います。
大学に落ちたので浪人することになり、予備校に通いました。この2年目の時は、もう少し、別の選択肢、alternativeについて検討していた節があります。いまは、博士課程進学ではない別のalternativeを、色々と俎上に載せては悩み、否定したり再考したり、というプロセスをやっている訳ですが、私の人生における、alternative検討の端緒を、この2年目の時に見つけられる気がします。具体的には、夏の段階で東大模試を受けて、ほんの一瞬だけ東大に行こうかと思ったり、センター利用でダメ元で早稲田の政経に出してみたり、というような程度のことですが。
結局、予備校に通っている間に物理が劇的に得意になったので、京大の物理工学科というところを受験し、合格しました。この時も、去年工学部を受けて落ちたので、工学部を受けるのだという理由以上のことは、特に考えていなかったと思います。また、物理工学科は入学後に2回生になってから5つのコースに分かれるのですが、その時まで詳細な進路選択の幅を、ある程度保留できるという気持ちもあったように思います。
私は都会の比較的裕福な家に育ち(たぶん中流家庭の上の方くらい)、それなりに多い教育機会を与えられて育ったと思います。小学生くらいの時は、母親や父方の祖父からは、よくあることかもしれませんが、とりあえず勉強しておけば、後でなりたいと思った時にある程度なりたい職業に就くことができる、という感じのことを言われて育ちました。まあ、いきなり野球選手とかになったりは出来ないと思いますが、ある程度は正しいのだと思います。一方、父親からは、私が1回目に大学に落ちた後に、進路のビジョンが無い、というようなことを言われました。それは、ある意味当たり前です。目的は問わず、とりあえず勉強しておけば良い、という感じで育つと、ビジョンが無いのは当然です。
こういうビジョン不在のまま、とりあえずここまで来てしまってから、いざ何か違うなとなって悩み始めているのが今なのかもしれない。そう考えると、これは幸福過ぎるが故の問題なのかもしれません。進路の可能性を保留し続けた結果、いよいよその戦略が限界にきていると言うこともできるかもしれません。
私が最終的に博士課程への進学する旨を指導教員に伝えたのは、昨年の9月ごろだったと思います。これは時期としては結構早いらしいです。理系修士を卒業した後の極めて一般的な進路は、どこかの企業や官庁に就職することだと思います。いまはある程度相対化していますが、父親からは公務員にはなるなという教育(?)を受けて育ってきたので、この時点では官公庁は進路として検討していませんでした。企業への就職としては、まず第一に考えられるのは、大学院までで身につけた「それなりの専門性」を評価する企業への就職です。修士1回の授業では、この専攻を卒業した人間が大体就職しそうな企業から毎週1人ずつやってきて、企業紹介をする授業がありました。結論から言うと、私はあまりそれらの仕事が自分事として捉えられなかったのです。真剣な興味が湧かなかったとも言えます。その点で、博士課程進学への決断は、ある意味決断ではなく、保留だったのかもしれません。
これらは消極的理由です。一方、博士課程進学を少なくとも一回は決断させた積極的理由は無かったのかというと、「真剣なその学問への興味」のような理由ではない理由はいくつか思い浮かびます。まず、博士号が欲しいということ、そして自分の名前が書かれた論文を出したいということです。いや、もしかするとその当時は「真剣なその学問への興味」、好奇心があったのかもしれない、もしそうだとすると、それは現時点では影を潜めている気がします。
最近の私には、明らかに昔と比較して認識上のある変化を感じています。それは強いショックを受けたか、あるいは継続的に環境から影響を受けたか、そのどちらかというと後者かもしれません。昔は、ある程度「道から外れずに」「きちんとした社会人」にならなければ、強い言葉で言うと、飢え死にするのではないか、という感覚を持っていました。しかし最近ではむしろ、そうした定常状態であるよりも、動的にチャレンジしていることの方が恐らく重要で、かつ楽しく、そういう状態である限り、飢え死にはしないと思える程度には、社会のことを信頼できるようになってきたような気がします。もちろん、戦争のような特殊な状況が訪れれば、話は一筋縄ではいかないのかもしれませんが。
でも、私の博士課程進学へのモチベーションはその程度のものだったような気がします。理系の博士号を持っていれば、恐らく徴兵されない。つまり死なない。ご飯に困ることもないかもしれない。いざとなれば、博士号を持っていれば、海外への脱出も容易かもしれない。そのような消極的な動機であれば、前提が変更されれば、動機が動機でなくなってしまうのかもしれません。
自分の名前が書かれた論文を出したい、という理由についても検討します。最近の私の論文というものに対する認識は、明らかに昔とは変わってきました。とても簡単に言えば、その昔、論文とは、非常に価値のあるものだと思っていました。価値があるからこそ、自分の名前の書かれた論文を出したい、と思うのであって、それほど価値のないものでも論文になってしまう、ということを知って、ある意味幻滅してしまったのかもしれません。世の中には学振という制度があります。博士課程の学生が生活費と研究費をもらうために申請書を書いて応募する制度です。そこには業績欄というものがあり、学会発表をしたり論文を書いたりすると、それが業績になります。業績はあくまで客観的な指標に過ぎません。それが本質的に重要なのかは疑問です。学振(特にDC1という博士課程に進学する前に応募するもの)には、業績のある方が採択されやすいという嘘か本当か分からない噂がありますが、学振を通すために、「革新的に重要」と呼べるわけではない研究成果を作って発表するために、落ち着いて振り返る暇もないまま、実験するのを急き立てられるのに、少し疲れてしまいました。このことは、私にとって、研究を今後このまま続けていって、それが楽しいのかどうか、ということに疑問を抱かせるに至っています。
何かをやっていて、感動できるか、心が動くか、ということは非常に重要だと思います。駿台予備校の石川正明先生は、最初の授業で「意味性、論理性、感動性」という象徴的な言葉を挙げていました。私はこの中で、感動性が特に重要だという気がしています。感動するから、心が動くから、それはどうなっているのか、という意味や仕組み、論理展開について興味が及ぶのです。今の研究室で研究を始めた当初は、実験試料を見て感動していました。なぜこんな色になるのだろう、と思っていました。そうした自発的な心の動きを取り戻さなければ、研究をやろうという気持ちに中々ならないような気がしてきました。あるいは、研究でなければ、そうした感動できることをしなければならないと思います。
自分はまだ、非連続的な変化を恐れているのかもしれません。非連続的な変化には、適応への失敗というリスクが伴います。遷移的な変化であれば、そのリスクを最小化できます。そういう意味では、alternativeは、常に検討し、育てなければならないものです。それに対しては、一つのことに集中していないという批判があります。実際、こうした批判を受けてから調子が悪くなりました。
そうしたもとで(急に日銀語調)、いつでも自立できるような、連続的に移行可能なalternativeを持っておくことが、私にとっては重要であるように思えます。人によって違うとは思います。しかし私にとっては、「初志貫徹」であるよりも、最新の状況に応じて思考を更新していく方が性に合っている、と思います。性に合っているということは、恐らく生存可能性が高い、とも思います。このあたりの考えが何由来なのかは分かりません。私の好きな人狼ゲームでは、盤面が更新される毎に認識も更新しなければなりませんし、私の好きな哲学であるプラグマティズムでは、そうした、状況に応じてより適切な認識に迫っていくという真理観が提唱されています。
面白い、感動することと、お金がもらえることは、一致させることがかなり難しいのではないかと思います。一撃でそれを実現する方法も恐らくない。リスクの海には飛び込めず、「初志」も貫徹できない以上、alternativeを成長させながら、何者かに迫っていくしかないのでしょうか。私が最近「まだ何者にでもなれそうな気がする」とよく言っているのは、このような拡散した、目的の定まらない、ビジョンを問い直している自己についてのことなのです。早く哲人になり、未来を見通したい。
これからの戦争と私
2024年の世界では、戦争が続いている。戦争の現場は、人権が抑圧、無視、毀損、破壊される現場である。日本もそう遠くない将来、いや、差し迫った直近に、戦争が起きる、戦争に巻き込まれる、政府が戦争を始める、戦争状態になる、気が付いたら戦争になっている、こうした状況になるという予感はあるし、こうした予感は日本社会において、ある程度共有されているような気がする。
自分の20代をどう生きるのか。戦時下は、非常時であるから、普通の、戦争が起きていない、平時と同じ生き方は出来ない。でも、出来るだけ平時の生き方を踏襲して、我々は戦時を生きなければならないのか?どうせ全て潰れて無くなってしまうという、当たるか当たらないか分からないが、そういう可能性がある状態で、普通の、真面目に生きていれば希望のある、そういう生き方をしなければならないのか?我々は、盲目的に、戦争が起きるかもしれないことに気付きながら、敢えてそれに目を瞑って、知らないふりをして生きなければならないのか?
もし戦争が起きて、今の社会で意味のあることが全て無意味になるような状況に突入する時、今の社会で、自分の人生のために頑張ることに、果たしてどれほどの意味があるのだろう。このような状況で、こうしたストレスから逃れる自然な道筋として、以下の2つが思い浮かぶ。
まずは、今の社会、この幸せな瞬間を噛み締める、という方法だ。どうせ全てが無意味になるのなら、今この瞬間に最も価値がある。刹那的に、今この瞬間を大事にする。
次は、もっと自暴自棄な方法だ。どうせ全てが無意味になるのなら、どうせ一回リセットされるなら、現世(今の社会)でどれだけリスクを取っても、リスクを取りすぎることはない。成功すれば破壊的に突き抜けるし、失敗してもリセットまで待てば良いだけ、というような、そういう選択をすることが、自然な選択として浮上する。
問題は、リセットが来ないかもしれないことだ。戦争はかなり来そうだけど、もしかしたら奇跡的に来ないかもしれない。そうすると、リセットは起こらない。取りすぎたリスクは、相応の報いとして自分の身に降りかかることになる。
戦争は来るかもしれないけど、もしかしたら社会を根底からひっくり返すような、そうした現れ方はしないかもしれない。中途半端な、どっちつかずな、あまり「面白くない」状態が続いて、それで終わるかもしれない。
いっそのこと、社会が完全に破壊されたら、「真面目に」平時の生き方をしなくても良いのに。退屈な、いつ壊れるとも分からない不安定な状態を続けなくてよいのに。でも、完全に破壊されたら、それはそれで選択の余地のない、限りなく生きにくい社会になるだろうな。
死にたくない。自分だけ生き残るみたいな発想にも意味はない。最後に逃げ場は残されていないはずだから。自由のために闘うのはかっこいい。国家権力と対峙するとアドレナリンが出る。国家と闘うと、国家に殺されるかもしれないけど。でも、国家と闘わなくても、国家に殺されるかもしれないよね。
研究室に行けなくなりつつ、仕事より生活の方が大事だと思いつつ、自分の進路を考えて悩みつつ、2024年の春。大きなことを成し遂げるか、普通の人生を生きるか。戦争というファクターは、重く、そこにある。
ネオ・プラグマティズム宣言 〜熊野寮から学生運動へ〜
熊野寮に何年も住んだ人間として、「自治寮の良さ・悪さ」、それらを包括した価値について、語らなければならないと思うようになってきた。自治寮については、世間に十分に理解されているとは言い難い。要因としては、いくつも考えられるだろうが、以下のような指摘もあった。
ものすごい問題点として、政治党派以外の人が大学自治や学生自治のコンセプトを一切言語化しないというのがありましてね…
— TCN (@TCN_Kyoto_TPU) 2024年2月19日
彼(彼女?)は、政治党派以外の人間が、大学自治や学生自治のコンセプトについて言語化しないことの問題性について述べている。学生自治寮における「自治」は、当然のことながら第一義的には、大学自治や学生自治の文脈の上にある。
私は政治党派(セクト)の人間が、寮自治論を語ることを何ら悪いこととは思わない。しかし、特定の政治思想をもつ人間たちだけが寮自治論を語り、そのほかの人間が沈黙しているような状況はまた、健全な状態だとは思えない。
熊野寮という自治寮に何年も住んだ人間として、そして多少とも寮運営の議論に関わり、セクトの活動家の主張も、ノンセクトの活動家の主張も、そして多くの「普通に大学で学んでいるだけの」学生の主張、これら全てに「バランス良く」関わった幸運な人間として、私は、次のような信念を持つに至った。
それは、寮運営の議論に関わる人間の念頭に、ネオ・プラグマティズムの考え方を置くべきだ、ということだ。
そう言われても、多くの人間には何のことかさっぱり分からないかもしれない。私は今、寮自治に関心があり、かつネオ・プラグマティズムに関心がある人間(ほぼ空集合では?)だけを想定読者に措定するという、この上ない過ちを犯したかもしれない。
しかも私は、大学で哲学を専門に勉強した人間でもない。しかし、この点に関しては、大学でマルクス主義を専門に勉強したわけではない政治党派の人間が、何となくそれっぽいことを言っている状況があるので、条件は対等だと思う。
また、哲学としてのマルクス主義は、歴史的にさまざまな批判を受けているが、運動・実践としてのマルクス主義運動には一定の力がある。ネオ・プラグマティズムもまた、哲学として歴史的にいろいろと批判されている。私の主張は、運動としての力の強さは、元になった理論の正しさとは実はあまり関係ないから、ネオ・プラグマティズムを理論として批判するのは自由だけど、運動・実践にはあまり影響しないかもしれないよ、ということだ。
加えて、ここが最も重要な部分だと思うが、ネオ・プラグマティズムが現在の哲学界において一定の影響力があるということは、少なくとも同時代に生きる我々にとっては、その主張がもっともらしく感じられる度合いが、結構高いのではないかということだ。ネオ・プラグマティズムの主張は、哲学を専門的にやっているわけではない多くの人間にとっても、それを「平易に」(ここで色々と捨象されるわけだが)説明すれば、結構潜在的に皆が考えていることと一致するものがあるのではないか、と思うのである。
それではそろそろ本題に入りたい。
私の理解では、ネオ・プラグマティズムの少なくとも実践哲学の部分からは、「異なる考え方を持つ人間同士の相互理解」を実現するためにはどのような「気持ち」を持てば良いのか、ということを学ぶことができると思う。そして、この点が自治寮の運営に関わる議論をする人間の、念頭に置くべきことだと私は考えるのである。ちなみに、ここで言うネオ・プラグマティズムの思想家とは、とりあえずローティやブランダムのことを想定している。
例えば、ローティは、『偶然性・アイロニー・連帯』という本を書いているが、ローティは(というよりプラグマティストたちは)、何か絶対的な真理があるという考え方を採用せず(マルクス主義と相性悪そう)、各人が色々な実践を行う中で、考え方がより正しいものに段々修正されていく、というような考え方をする。さらに、そのような考え方においては、自分が今たまたま持っている(「偶然性」)信念も、絶対的に正しい訳ではないから、間違っている可能性があり、自分が普段抱いている信念を疑いながら過ごすことが求められる(「アイロニー」)。そうした態度は、自分の考え方を絶対視しない点から、逆に、いま自分が持っている信念とはそぐわない信念を持っている相手の考え方が、実はより正しいものである可能性があるのではないか、という思考に可能性を拓く。つまり、このようなローティの論に乗っかれば、プラグマティズムの考え方を部分的にでも採用することで、自分とは前提が異なる相手のもつ信念を、ある種尊重するような態度を育むことができる。それは、異質な他者との間の相互理解への端緒を拓く点で、「分断」を回避し「連帯」を実現することに繋がる。
「連帯」の重要性は、少なくとも寮運営に主体的に関わっているセクト・ノンセクトを問わない活動家には言うまでもないはずである。
同時に、上記のような思考態度は、普段セクトの活動家に一方的に思想的に勧誘(オルグ)されて辟易としている「普通の学生」にとっても、その価値を理解できるはずである。
もう一つ、プラグマティズムを寮自治運営の議論の場に適用する上で示唆的な例を見てみよう。
たとえば、「渡り鳥のための湿地帯を保護する」という場合、そのような環境運動に参加する人々には、さまざまな理由があるだろう。人間中心主義者なら、狩猟を楽しむため、生命中心主義者なら、感覚を持つ個体を尊重することの重要性、等々。このように、何を重視するかという価値観や世界観のレベルで意見に深刻な対立がある場合、これらの人々は決して連帯し、団結することはできないのだろうか?
環境プラグマティストのノートンによれば、決してそんなことはない。具体的な実践では、こうした対立は解消できる。むしろ理論的な対立にこだわって何もしないより、具体的な政策において一致団結すべきであると説くのである。
プラグマティズムは一般に、それぞれ異なるとされる信念であっても、結果としてそれらが同じ行為を導くのであれば、その信念の差異を問うことには意味がないと考えるのである。
こうした議論は、寮自治運営の議論にも適用できるだろう。すなわち、寮を誰にとっても住みやすいものにするための施策で結果的に一致できるのであれば、それを支持する個々人が、どのような思想を持っていても、その差異を問うことは無意味であると、プラグマティズムは教えるのである。
これらは、(ネオ・)プラグマティズムの考え方を、寮自治運営の議論に参加する人が持つことの重要性を示す、一例に過ぎない。プラグマティズムを勉強すれば、その考え方が寮自治運営の議論に参加する上で重要だと理解できるはずだ。プラグマティズムという150年近いアメリカ哲学の伝統に立脚することで、我々は、自分たちの住んでいる場所を、自分たちでもっとより良いものにしていくこと(自治!)が必ず出来ると私は信じる。それは熊野寮のみならず、広く学生寮、学生・大学自治から、ひいては「この国の在り方」に至るまで、長く広い射程をもったものであるはずだ。
最後になるが、「ネオ・プラグマティズムの学生運動」は、原理的に新しい。なぜなら、何をネオ・プラグマティズムの最初とするかはいろいろ説があるが、ローティ『哲学と自然の鏡』以降だと考えると、この本の出版は1979年であるからだ。世界的に学生運動が盛り上がったのは、1968年のことであり、ネオ・プラグマティズムは、いわば「全共闘以後」に登場してきた思想である。まだ、「ネオ・プラグマティズムの学生運動」は十分に実践されていない。だからこそ、そこに可能性があると私は思う。
私の学生としての寿命は長くない。老兵は死なず、ただ消え去るのみなので、誰かやってみて欲しいという気持ちと、仲間が見つかるまでとりあえず私だけでもやってみようという気持ちと、半々くらいである。
参考文献:
岡本裕一朗『ネオ・プラグマティズムとは何か ポスト分析哲学の新展開』(ナカニシヤ出版,2012)
NHK「100分de名著 ローティ『偶然性・アイロニー・連帯』」
山に登る 心境の変化
むかし、なぜ山に登るのか、ということについて、書いたことがある。その時と今とでは、全く同じ感情を感じているというわけではない。最近山に登って、最近山に登った時はこういうふうに感じているなと思ったことがあるので、そのことについて書くこととする。
習慣的に登山をするようになって、もう10年近くになる。最初は、高校の山岳部に入ったことがきっかけで、高校を出た後も、いろんな人と、時には一人で、山に登っている。私との登山がきっかけで、登山靴を買ったという人も何人かいる。中にはアイゼンを買った人もいる。
最初の頃は、アルプスで森林限界に出た瞬間とか、景色がよく見える山頂に来た時とか、そういう時が楽しかったし、今でもそういう気持ちは持っている。けれど、最近では、明らかに昔だったら感じないような感情を感じるようになっていて、そうした変化を感じている。
例えば去年、一人で霧島連山に登った時、下山する時に、これは最初から分かっていたのだけれど、駅まで車道を10km歩かないといけないことがあった。そうすると途中で、トラクターに乗って何かやっているおじいさんがいて、ふと目が合うと、少し話したりする。孫に似てると言われたりする。そんな何分も話さないけど、こうやってよく覚えていたりする。
またこないだ、何人かで雪が少し積もる大和葛城山に登った帰り、駅まで3kmくらい歩いていた時、ふと広がる何でもない畑か田んぼか、何となく良いなあと思ったりする。段々畑の写真を何枚か撮ってみたりする。こういうことは前から思っていたのかもしれないけれど、最近よく覚えているようになった。
ずっとやっていても、異なる気持ちを感じたりする。そういう心の変化を感じ取りたい。掬い取りたい。それを文章にしておくことは、後から振り返った時に、とても価値あることだと感じられる。その一瞬を、いま掴み取らないと二度と手に入らない感じを、最近結構やっているので、もう少しゆっくり行きたいと思う。
2024年のビットコイン投資方針
2023年は対USD、対JPYともにBTC価格は約2.5〜3倍の単調増加であった。2024年も変わらず、Buy and Holdを貫いていく。(BTCのBuy and Holdにはかなりの「信念」が必要だと思う。)
一方で、当たるも八卦当たらぬも八卦、の占いを年初にやっておくのも悪くないと思ったので、読者の皆様に認識を開示しておきたい。私が将来、振り返ることを兼ねている。
結論からいうと、私の予想は、BTC/USDのATH更新は、多くの人が予想するように、2025年にもつれ込むのではないかというものだ。それでは、巷の半減期論と何も結論が変わらないが、もう少し考えた上での結論である。なお、認識とは時々刻々変化するものであることはお忘れ無く。
一応、過去のピークの頂点を見ておくと、前回が、2021年の11月ごろ、その前は2021年の春先である。この2つは纏めて良いだろう。その前が、2017年の12月であった。半減期論とは、BTCの半減期が4年に一度であることを踏まえ、新規供給量の減少がBTCの希少性の上昇につながることから、BTC価格の高騰と関係するという主張である。
これまでの半減期は、2016年7月、2020年5月だったらしい。次回は、2024年4月頃と予想されているらしい。いずれも、半減期の1年後くらいに、ATHになっていることから、次のATHは2025年という予想が一般的である。
それでは、ここからは私がATHが2025年にもつれ込むのではないかと予想する理由を述べていく。
2024年は名目金利が下がりそうだ。インフレ率が据え置きの場合、実質金利も下がることになる。これは金価格に対して肯定材料である。BTCの性質がゴールドと似ていることを踏まえると、BTC価格の推移予想にゴールド価格の予想を参照することにはそれなりの合理性があると思える。
一方、2024年または2025年は、FRBの金融引き締めの効果がそろそろ現れて、株式市場と実体経済にそろそろダメージが入るのではないかと予想されている。その場合、金価格は、リーマンショックの時にそうであったように、一時的に下落することになる。BTC価格が金価格に連動するなら、BTC価格も下がるだろう。
メカニズムは、以下の通りである。すなわち、金融危機が起きると期待インフレ率が下がる。すると、実質金利が上がる(実質金利=名目金利-期待インフレ率)。実質金利の上昇は、金価格にたいして不利であるから、金価格が下がる。
すなわち、2024年は、名目金利減少と、株式市場崩壊による期待インフレ率の減少という二者の要素のせめぎ合いになる。これは、金価格に対しては、それぞれ上昇要因と下降要因である。よって、2024年の金価格は、単調的な振る舞いを見せないだろうし、BTC価格が金価格に連動するとすれば、BTC価格もまた、単調な振る舞いを見せないのではないか。レンジ相場である。
では、その後はどうか。株式市場が崩壊すると、FRBは金融緩和を強めざるを得ないだろう。すなわち、名目金利の低下である。それが意味するところは、インフレの亢進であり、期待インフレ率の上昇である。これらはいずれも、実質金利の低下要因となる。金価格またはBTC価格は、上昇するだろう。こういうことは皆、2025年に起こるのではないか。
一方で私は、みなさんにはBTCを持つことを勧めない。将来的には、BTCを持つことは犯罪になるだろうからだ。詳しくは、以下の記事をお読みいただきたい。
philosophiaichi.hatenadiary.jp
人間が宇宙へ行くというモチベーションは持続するか
小学校の頃は、クラスで宇宙と言えば私、で通っていたし、実際、天文ではなく宇宙開発の方に興味のある子どもだった。そうした小学校高学年時分に抱いた素朴な思いは、中学・高校で定期テストと受験のための勉強に焦点があっていく中で、知らずのうちにどこかへ追いやられた。大学へ入ってからも、大学一年時のほんの一瞬だけ、宇宙太陽光発電に興味を持った時があったが、結局進む進路も宇宙系は選ばなかった。その中でも、底流として、宇宙というキーワードは私の中に存在して、たまたま目の前に現れた機会に出会い、いま少し宇宙開発に関わらせてもらっている。それ自体は非常に幸運なことではあるが、私の「本来の」専門分野は、宇宙とは別のことであって、この先の人生において、宇宙方向に進んでいくかということは、まだ分からない。
ある人間の専門分野、職業の選択ということに関しては、当然その職業が今後存在するかとか、その分野がこれからも盛り上がっていくか、ということを十分に考慮に入れて、色々と決断していくものと思う。従って、本分は本業に置きながらも、応用として宇宙に関わるというやり方も、あるかもしれないとは思う。いずれにせよ、そういうことを考えるにあたって、宇宙産業はこれからも伸びていくのか、という人によってはほぼ答えが自明であるように感じられるかもしれない問題を、自分ごととして考えなければならない。
最近は、特にアメリカで民間企業の宇宙進出が極めて活発になっているし、宇宙を利用した産業ということもかなり話題となっている。宇宙といっても色々あって、地球にごく近い部分から、月や火星、さらにもっと深宇宙まである。近年言われている宇宙利用産業の多くは、ごく地球近傍領域の話だと思う。一方、イーロン・マスクなどは火星に人を送り込むというような話をしているし、現在出ている産業的な宇宙の話の一番遠いところは、火星くらいかなと思う。
では、その火星に行くとして、一体何が嬉しいのか、ということを明らかにしたい。資本主義の論理で言うと、投資した資金は多少増えて回収されなければ、投資する主体がいなくなってしまうから、火星に行くことによって、それに関連して派生する技術でも何でも良いので、何か金になるリターンが無いと、火星への投資というモチベーションは次第に失われて、持続しないものになるだろう。
宇宙とはフロンティアであるから、過去同様のフロンティアに人間が出て行った例を考えたい。例えば大航海時代以降続く時代では、ヨーロッパ各国は、アジアやアフリカにある天然資源や人的資源(奴隷)を目的として、フロンティアに出て行って、それは莫大なリターンを産んだので、資本主義として投資のサイクルが継続した。あるいは、アメリカなどは元々いた先住民を虐殺してヨーロッパ人が住み着いた訳だけれども、そうして人が一旦住み始めると、それ自体が需要となって、発展していくということもあるかもしれない。宇宙に住むのは、色々な意味で17世紀のアメリカに住み始めるより、かなりの困難が伴うと思うが、技術で解決できる話なら、宇宙の方が住み心地が良いと感じる人が現れれば、そうして発展していくことはありそうだ。
冷戦期のアメリカとソ連は、両方ともかなり熱心に宇宙開発をやり、アメリカは月にまで行った訳だが、これは大陸間弾道ミサイルで核兵器を撃ち合える技術をお互いに確立した後は、それほど熱心に宇宙開発は行われなくなった。宇宙開発自体が目的ではなかったので、投資は続かなかったし、その競争に耐えきれなくなってソ連は崩壊してしまった。
よく宇宙にはロマンがあるとか、夢があるとか、言われる。それは宇宙にロマンや夢がある人たちがそう言っている訳なので、その人たちにとって宇宙に夢やロマンがあるのは当然である。しかし、夢やロマンだけでは、とここまで書いたところで、モチベーションと現実的な条件を考えるということについて、少し混乱してきた。
京大の宇宙ユニットは、宇宙進出の現実的可能性について考える研究者の集団で、本を何冊か出している。
『有人宇宙学: 宇宙移住のための3つのコアコンセプト』(山敷 庸亮)の感想 - ブクログ
『人類はなぜ宇宙へ行くのか (シリーズ〈宇宙総合学〉 3)』(土山明)の感想(4レビュー) - ブクログ
KULINEで目次を見てみると、結構多くは、どうすれば現実的に宇宙に継続的に住めるのか、というその方法について議論しているように見える(まだ読んでいないので分からないが)。今は、イーロン・マスクなどの動きもあるし、衛星などの地球近傍宇宙での活動はすぐ商売に結びつくだろうので、人間がなぜ宇宙に行くのか、そのモチベーションが果たして持続し得るものなのか、ということをあまり考えないでも、それは所与のものとして、ちゃんと宇宙で過ごせるための条件だけ考えれば良いということになっているのかもしれない。実際、宇宙で過ごせるための技術的条件無くしては、ロマンだけあっても住めないので、そのこと自体は極めて重要である。
投資も、一面的には持っているロマンを実現するために資金を投じるという性格は否定できないが、全体として見たときに、投資のリターンが小さい状況では、資本を投下する主体はだんだん少なくなっていって、持続できないものになるかもしれない。
最も安価な回答は、夢やロマンかもしれない。こうした「哲学的な」問いを、自分の進む道に照らし合わせていけるのは、結構面白い。私の2020年代はこういう感じなのかもしれない。後期は宇宙の授業をいくつか取る予定なので、こうしたことについて考えたいと思う。
資本主義の終焉・分断と対話・個人
最近、資本主義の終焉ということの意味が分かってきた。
身近な共産主義者たちが、金融資本家は追い詰められていて、この社会をプロレタリアートの連帯によって実力で変えられるんだ、という話をよくしている。
世界最大のヘッジファンド、量的緩和と現金給付に続く新たな金融緩和を語る | グローバルマクロ・リサーチ・インスティテュート
私は、このグローバルマクロ・リサーチというブログから、経済変動についての考え方の示唆を受けた部分が大きい。グローバルマクロ・リサーチを書いている人は、よくハイエクを引用する。オーストリア学派的な経済の見方をしていると思う。
グローバルマクロ・リサーチは、よく以下の図を引用する。
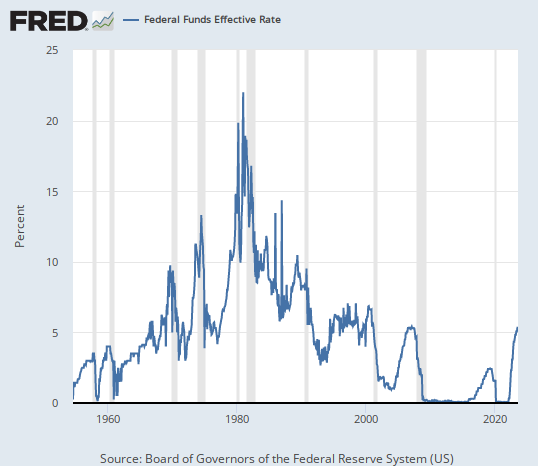
この図は、米国FRBの政策金利が、石油ショック以降、約40年にわたって右肩下がりであるという図である。
ところで、銀行というのは資本主義の中心にある仕組みであり、マレー・ロスバード的な考え方かどうかは少し自信が無いが私がそう思っている考え方では、米国FRBを牛耳る国際金融資本家は、資本主義の中心に位置して、ペンを動かすだけで(貨幣発行権を有するだけで)座っていても富が集積してくる。ロスチャイルドとかが言ってそうなことである。ロスバードの考えでは、中央銀行と政府を一体的に牛耳る権力の近くにいればいるほど、そのおこぼれで確実に儲かるのであって、それはフェアな競争では全く無いから、リバタリアン的な見地から批判を加えているのだと思う。
実際、東京オリンピックとかを見ていても、政治家に近い企業が儲かっているのは自明だし、例えば開発をする時に、政治家の身内がたまたま土地を持っていたりしているらしいことを見ても、この議論には説得力があると思う。
こういう国際金融資本家を悪として強調する見方は、ユダヤ陰謀論とかなり親和性が高いし、革命的左翼党派の共産主義思想も、何となく見ていて陰謀論と親和性が高そうな気がする。当事者たちは、実力で社会を変えられると思うのが我々で、悲観的なのが陰謀論だ、とよく言うけれど。
そういう訳で、40年間にわたって金利が右肩下がりなのは、資本主義が段々儲けられなくなってきていることの証左だな、と最近思った訳である。
資本主義の終焉と歴史の危機 – 集英社新書
少し調べてみると、全く同じ話を考えている人は当然いて、水野和夫『資本主義の終焉と歴史の危機』という本を見つけた。この水野という人は、私の記憶違いでなければ、金融系のTwitterでたまに批判されていると思う。いわゆる「トンデモ系」であるという評価が多い。まあ、主張内容は異端であるから、正統とは相容れないのだろう。私は読んでいないから、よく分からないけど。
日銀破綻論を唱える藤巻健史や、河村小百合も、たぶん似たような界隈からはトンデモだと評価されている。私はあまりそうは思わないので、この辺りの評価の具合は、評価する人の、立場や主義に依存する部分が大きいように思う。
続いて、グレート・リセットの話を。
革命的左翼党派の共産主義者たちがよく言っている見方では、資本家階級は、何回か資本主義を延命してきたという。つまり、今までも、これ以上儲けられないとなって、限界に当たってきたが、そのたびに例えば戦争を引き起こしたりして、一度全てを更地に戻せば、もう一度「成長」することができる。「成長」すれば、再び儲けることができるので、資本家階級にとっては、万々歳ということになる。
最近、陰謀論や都市伝説の界隈では、「2025年にグレート・リセットが来る」ということが、しきりに強調されている。
コヤッキースタジオ - YouTube
都市伝説に全く素養の無い人は、「巷に転がる都市伝説紹介チャンネル」のコヤッキー・スタジオとかを見て欲しい。
私の感覚では、この「グレート・リセット」とは、多分戦争とかなのだろうと思う。逆に、戦争じゃなかったら、驚くくらいである。
都市伝説や陰謀論は、こうした政治や経済の難しい話を理解できない層に、エンタメとして世の中の動きを消化させ、理解させるというような働きをしているのかなと思う。
世間では、トランプ大統領が出てきた頃から、「分断」というキーワードが強調されるようになった。
曰く、社会が分断されている。相互に理解や意思疎通が出来なくなっている。極右や極左が力を持ってきている。
これは、社会をマクロで見た時に、社会に「分断」が生まれているということだと思う。
ミクロとマクロの議論が直線的に繋がるとあまり思うべきではないと思うが、自治空間における日常的な政治の風景にも、やはり分断というものがある。ミクロな、個人レベルにおける、分断。相互理解の不在。敵対。政治的対立。対話の不成立。
そして、このミクロなレベルでも、この分断を解消するのは極めて骨の折れる仕事であると、私は最近認識するに至った。
私は、世間の並の人間と比べると、かなり政治的に「意識の高い」(リベラルという意味ではない)人間だと思うが、それでいても、私が自治空間の政治的秩序の維持に割くコスト・パワーの大きさを思うと、少し尻込み・躊躇をしてしまう。
ミクロなレベルでさえもこうであるのだから、マクロなレベルの分断を解消するなんて、ほとんど不可能に思えてしまう。対話の方法や、技術で何とかなる問題でもないと思う。誰かどうしたらいいか知っていたら教えて欲しいし、誰もやり方が分からない(知識人でも分からない)からこそ、いま世界中で問題になっているのだと思う。
こうした、ミクロな身近な生活のレベルの政治において無力感を感じた人間の向かう先は、ただ個人の発展であって、私もいまそうした傾向を持っている。しかし、周りを見渡すと必ずしも、そういう人間ばかりではないと見える。私はかなり珍しい部類のようだ。
3パターンに分けてみよう。
1、社会や(身近でさえも)政治に対して向かうのではなく、個人を発展させよう
2、社会や政治を個人の力で変えよう
3、何もしない(あるいは、どうせ「グレート・リセット」で全てが無意味になるので、何をしても意味ない)
1が今の私。2が、ある革命的左翼党派の共産主義者たち。3が、そのほか大勢。
今の私は、自分個人の実力を高めることに(何らかの)意味があると、素朴に信じられているのだと思う。しかし、戦争(グレート・リセット)という個人ではどうしようもない(3の立場)ことが、降りかかってくる中で、個人の実力みたいなものにどれほどの意味があるのか、と考えてしまうことが無いとは言い切れない。1の立場は、そうした不安定さがあると思うし、だからこそ「珍しい」のだなと思う。